亲们QQ飞车雷诺怎么得?
的有关信息介绍如下:方法/步骤
1.首先,登录飞车客户端,进入主界面。

2.QQ飞车里雷诺是可以直接购买使用的,而且相对其他A车来说价格并不高,而且雷诺可以说是稳定性很好的一辆车了。

3.进入游戏后,第一种方法是直接购买,点击进入商城,搜索栏搜索雷诺,即可出现雷诺购买界面。
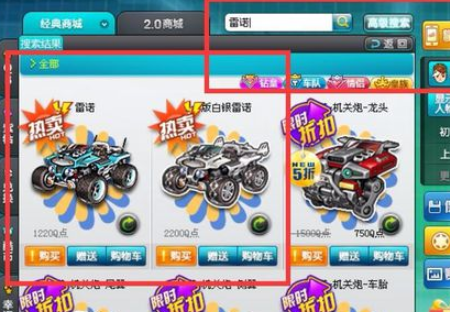
4.雷诺价格为12800点券每180天,也就是半年,建议如果要买,就买半年的,因为这个价格相对三十天的,九十天的都是优惠了不止一点。
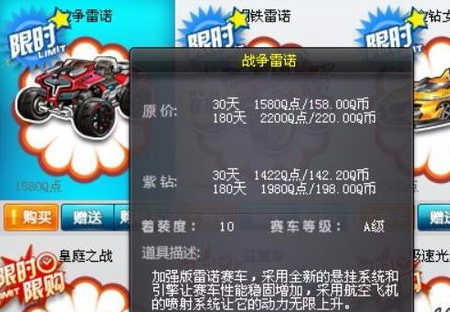
5.现在活动送雷诺的已经很少了,因为雷诺现在很普及,在以前飞车还没有那么多活动的时候,虽说雷诺价格亲民,但是价格也不低。

6.还有一种方法获取雷诺的,参加活动,不过现在很多活动不送雷诺,而是送雷诺的升级版本——黄金雷诺。黄金雷诺不仅在外表上惊艳了很多,而且喷口也由四个改成了五个。
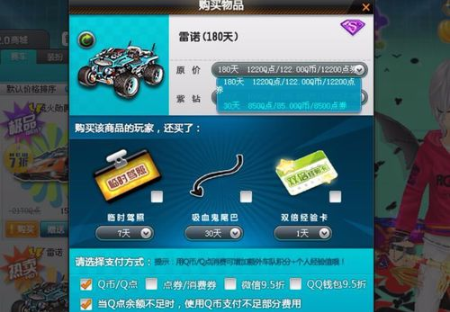
7.雷诺后来推出了全套改装配件,在商城都可以购买,配件可以用QB购买。




